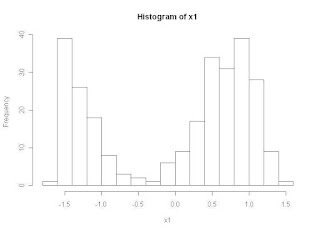
EMアルゴリズムの実装。
PRMLでは2次元の正規分布を例として扱っている。
この式は
が、ここではよりシンプルにするためにx軸のみ、つまり1次元のものを使う。
この式は
（Ｒのコンソールに直接張り付ければ良い）
結果は
nb of iteration 14
**** distribution 1 ****
mean: -1.286364
variance: 0.04316987
pi: 0.3488136
**** distribution 2 ****
mean: 0.6890519
variance: 0.1457242
pi: 0.6511864
log likelihood収束のようす
c( rnorm(400, 10, 2), rnorm(100, 2,1) )
Example 8.41: Scatterplot with marginal histograms (function of the plot with histogram)
R: 24. apply() ファミリー（このせつめい十分）
多変量正規分布（pdf）
混合ガウスモデルとEM（コードはこれをもとにした）
EMアルゴリズム答え合わせ（こちらも少し参考に）
EMアルゴリズムによる混合分布のパラメーター推定の解析計算＆実装例 from 「Rによるモンテカルロ法入門」（下のリンクとスライドを参考にした）
都市生活学・ネットワーク行動学研究室のPRML合宿2009（良く見ていないがまとまっていそう）
PRML 読書会 #12 ９章 ＥＭアルゴリズム＆１０章 変分ベイズ（下に英語pdfリンク）
PRMLでは2次元の正規分布を例として扱っている。
この式は
が、ここではよりシンプルにするためにx軸のみ、つまり1次元のものを使う。
この式は
コードは以下のようになった。
# -------------------------------------------------
# descripton
# name : 1d normal distribution
# -------------------------------------------------
# ***********************
# sub functions
# ***********************
# normal distribution
# same as dnorm() but using var instead of sd
normDist <- function(X,mu,vari) {
1/sqrt(2*pi*vari) * exp( - (X-mu)^2 / (2*vari) )
}
# log liklifood (posterior probability)
logLikelihood <- function(X, mu, vari, Pi, K)
{
Sum <- 0.0
N <- length(X) # number of data
for(n in 1:N)
{
tmp <- 0.0
for(k in 1:K)
{
tmp <- tmp + ( Pi[k] * normDist(X[n],mu[k],vari[k]) )
# Note: "log" computes natural logarithms
}
Sum <- Sum + log(tmp)
}
return(Sum)
}
# ***********************
# main computation
# ***********************
# -----------------------
# Prepare data
# -----------------------
# load Old Faithful dataset, and normalize
data("faithful");
xx <- scale(faithful, apply(faithful, 2, mean), apply(faithful, 2, sd));
X <- xx[,1] # take only the first column this time.
X <- scale(X) # normalize, so that mean is 0 and var is 1. (why necessary?)
N = length(X)
# nb of distribution
K <- 2
# initialize the parameters
mu <- 0
# Note: vari <- mat.or.vec(1,K) can make zero matrix but in R
# increasing the array length in loops is OK, so it is not necessary
# to write like this.
increment <- 2/(K-1) # 2 is from 1 - (-1)
for(k in 1:K)
{
# separately distribute between (-1, 1)
mu[k] <- -1 + increment*(k-1)
}
vari <- 0
for(k in 1:K)
{
# set to 1 for all distribution
vari[k] <- 1
}
Pi <- 0
for(k in 1:K)
{
Pi[k] <- 1/K
}
# for analysis
mu_initial <- mu
Pi_initial <- Pi
# prepare responsibility
resp <- mat.or.vec(N,K)
# compute initial log likelihood
like <- logLikelihood(X, mu, vari, Pi, K)
# initialize
likearray <- 0
nbIteration <- 1
while(1)
{
# -----------------------
# E-step:
# compute the responsibility with the current parameters
# -----------------------
for(n in 1:N)
{
# prepare denominator
denominator = 0
for(k in 1:K)
{
denominator <- denominator + Pi[k] * normDist(X[n], mu[k], vari[k])
}
# compute responsibility
for(k in 1:K)
{
resp[n,k] <- Pi[k] * normDist(X[n], mu[k], vari[k]) / denominator
}
}
# -----------------------
# M-step:
# recompute the parameters with the computed responsibility.
# -----------------------
# initialize
mu_new <- 0
vari_new <- 0
Pi_new <- 0
for(k in 1:K)
{
# compute Nk
Nk <- 0.0
for(n in 1:N)
{
Nk <- Nk + resp[n,k]
}
# recompute mean
mu_new[k] <- 0.0
for(n in 1:N)
{
mu_new[k] <- mu_new[k] + resp[n,k] * X[n]
}
mu_new[k] <- mu_new[k]/Nk
# recompute variance
vari_new[k] <- 0.0
for(n in 1:N)
{
vari_new[k] <- vari_new[k] + resp[n, k] * (X[n]-mu_new[k])^2
}
vari_new[k] <- vari_new[k]/Nk
# recompute mix ratio
Pi_new[k] <- Nk/N
}
# -----------------------
# judge of convergence
# -----------------------
like_new <- logLikelihood(X, mu_new, vari_new, Pi_new, K)
Diff <- like_new - like
# debug
likearray[nbIteration] <- like
like <- like_new
mu <- mu_new
vari <- vari_new
Pi <- Pi_new
#if(nbIteration == 20)
if(Diff < 0.01)
{
# print
cat("nb of iteration", nbIteration, "\n")
for(k in 1:K)
{
cat( "**** distribution", k, "****", "\n") # paste() is not necessary
cat( "mean: ", mu[k], "\n")
cat( "variance: ", vari[k], "\n")
cat( "pi: ", Pi[k], "\n", "\n")
}
break
}
nbIteration <- nbIteration + 1
} # close "while(1)"
# ***********************
# Dispaly
# ***********************
# -----------------------------------
# likelihood conversion bihavoir
# -----------------------------------
windows()
plot(likearray, type="o")
title("likelihood bihavoir")
# -------------------------------------------------------
# original data and the estimated mixed distribution
# -------------------------------------------------------
windows()
hist(X, breaks=seq(-3,3,0.2), xlim=c(-3,3), ylim=c(0,1), freq=FALSE,
main="", xlab="", ylab="")
a <- seq(-5,5,length=1000)
for(k in 1:K)
{
par(new=T)
plot( a, dnorm(a, mu[k], sqrt(vari[k]))*Pi[k], xlab="", ylab="",
xlim=c(-3,3), ylim=c(0,1), type="l", col=k+1)
}
title(main="data and estimation", xlab="x", ylab="density")
結果は
nb of iteration 14
**** distribution 1 ****
mean: -1.286364
variance: 0.04316987
pi: 0.3488136
**** distribution 2 ****
mean: 0.6890519
variance: 0.1457242
pi: 0.6511864
log likelihood収束のようす
- 初期値の影響
muの初期条件で、十分に離れているものをとると、尤度は単調に増加し、早く収束する。（ここではPiは0.5, 0.5としている）
左: 0.979, 0.011
右: 0.516, 0.861
わかるように、muは均等に配分することで、ずっと早く収束する（コード参照）。
c( rnorm(400, 10, 2), rnorm(100, 2,1) )
- 参考サイト
Example 8.41: Scatterplot with marginal histograms (function of the plot with histogram)
R: 24. apply() ファミリー（このせつめい十分）
多変量正規分布（pdf）
混合ガウスモデルとEM（コードはこれをもとにした）
EMアルゴリズム答え合わせ（こちらも少し参考に）
EMアルゴリズムによる混合分布のパラメーター推定の解析計算＆実装例 from 「Rによるモンテカルロ法入門」（下のリンクとスライドを参考にした）
都市生活学・ネットワーク行動学研究室のPRML合宿2009（良く見ていないがまとまっていそう）
PRML 読書会 #12 ９章 ＥＭアルゴリズム＆１０章 変分ベイズ（下に英語pdfリンク）
of observed data, a set of unobserved latent data or 
, and a vector of unknown parameters 
, along with a 
, the 
:![Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) = \operatorname{E}_{\mathbf{Z}|\mathbf{X},\boldsymbol\theta^{(t)}}\left[ \log L (\boldsymbol\theta;\mathbf{X},\mathbf{Z}) \right] \,](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_u2U5SOjdd_Kvxn8bMPqmcrmoaywEiAGXfXUWLqssjRpOpyQNBOjuaj8XVJyWRC76cGmasGv1KzN6jnYhJLbnvOD_Xnp3r4N-alZ3BLCGGqRhmBMuikUbjl5XPJzReV8qM6r3XErcnH_MYBuwdjTQ=s0-d)
